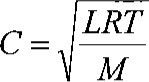
The speed of sound in still air can be measured accurately between two points a few centimeters apart by two ultrasonic transducers set at that distance. The resulting speed of sound is a known function of the air temperature and composition.
The speed of sound waves in an ideal gas may be written.
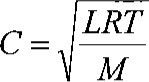
where R is the universal gas constant (0831.34 mJ/mol K), T is the temperature in Kelvin, M is the molecular weight (grams/mol) of the gas, and L is the ratio of heat capacities Cp and Cw Cp and cv are the specific heats at constant pressure and constant volume of the gas, respectively.
The transit time of a sound signal traveling from one end of a sound path to the other, separated by distance d, can be written as follows (Schotland, 1955):
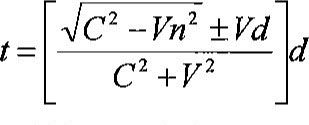
where V is the total velocity, are velocity components in the directions parallel and normal to the sound path, and C is the velocity of sound in still air. If two transit times, t, and t2 in opposite directions on the same path are directed, can be obtained independent from V and Vn as follows:
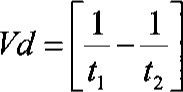
It is this principle that is used to compute the velocity of the air in the path between two opposing transducers.
In still air, ti and t2 are equal. For a distance 15 cm at 200 C, the transit time is approximately 450 vs. If a 20 m/s wind is in the direction of the sonic pulse, the transit time ti will be approximately 427 vs. If the wind is opposing the sonic pulse, the transit time will be approximately 482 vs. If these two values are used in the previous equation, the resultant velocity from equation will be 20 m/s.




Designed with
Mobirise